I.MonitoringSkiPaths(题解)xiaodangao

题目链接:I.Monitoring Ski Paths
思路:标记所有起点,有一个很明显的贪心就是从下往上找,碰到第一个标记的起点,就将其标记,但是这样会出现一个问题:

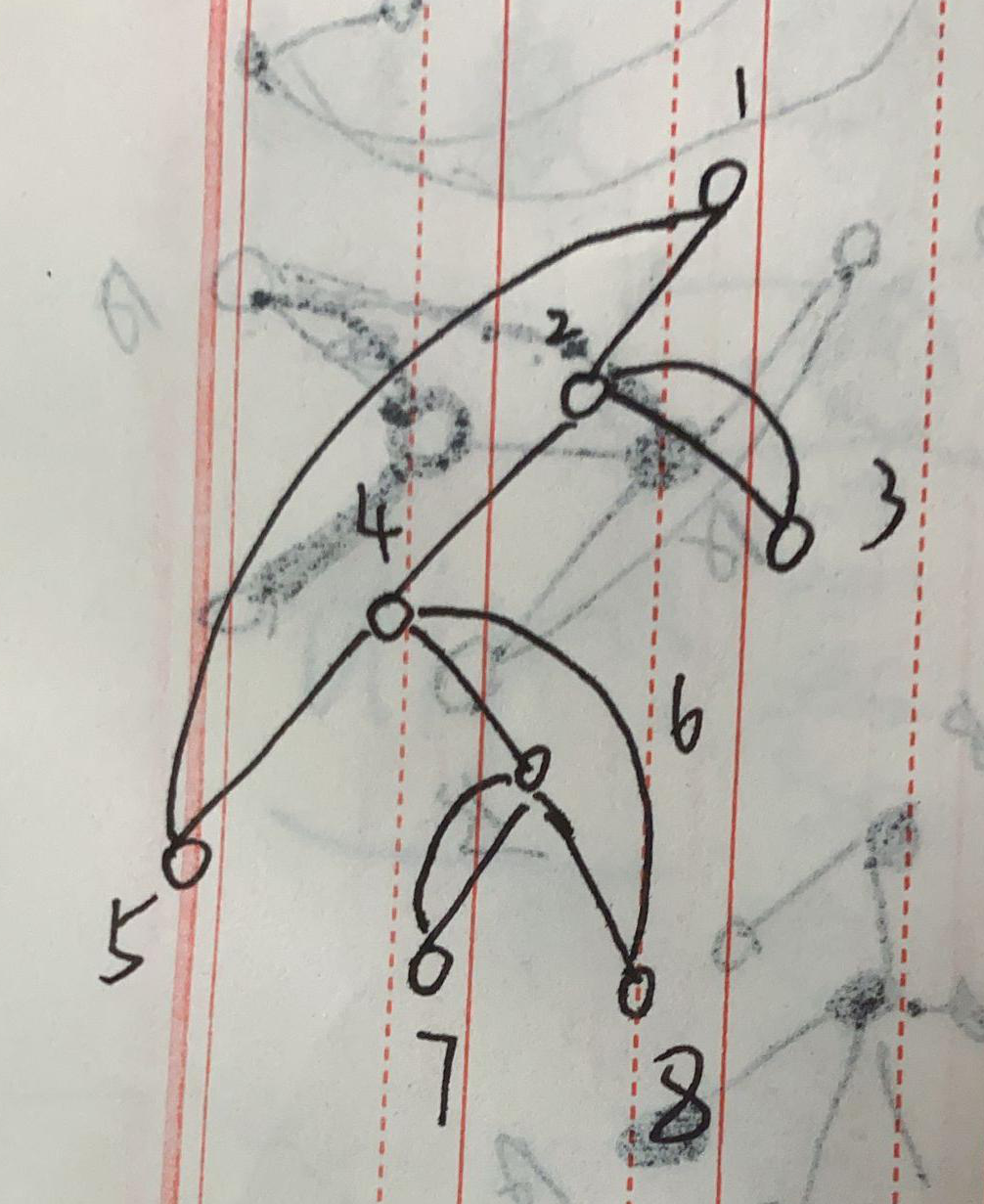
会发现如果先遍历5这个节点,会导致4被标记,然后答案就错了.这是因为6 - 7 4 - 8这两条边被6给标记后,4这个节点就没用了,所以我们优化我们的贪心,即:将所有边通过起点出现的深度进行排序,优先遍历深度深的起点所连接的终点,遍历之后,将所有该终点所连接的起点取消标记.因为是棵树,所以我们遍历时可以通过并查集的方式,因为这中间可能有很多空点,所以利用并查集可以优化遍历找起点的时间.
$Code:$


#include<set>
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<map>
#include<algorithm>
#include<vector>
#include<queue>
#define ch() getchar()
#define pc(x) putchar(x)
#include<stack>
#include<unordered_map>
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define ll long long
#define ull unsigned long long
#define pb emplace_back
#define mp make_pair
#define PI acos(-1)
using namespace std;
template<typename T>void read(T&x){
    static char c;
    static int f;
    for(c=ch(),f=1; c<'0'||c>'9'; c=ch())if(c=='-')f=-f;
    for(x=0; c>='0'&&c<='9'; c=ch())x=x*10+(c&15);
    x*=f;
}
template<typename T>void write(T x){
    static char q[65];
    int cnt=0;
    if(x<0)pc('-'),x=-x;
    q[++cnt]=x%10,x/=10;
    while(x)
        q[++cnt]=x%10,x/=10;
    while(cnt)pc(q[cnt--]+'0');
}


const int N = 3e5+10;
int n,k,m,v,u,depth[N];
vector<int>p,G[N],h[N];
pair<int,int>a[N];
int fa[N];
bool ok[N],vis[N];
int st[N];
int found(int x){
    if(ok[x] == true or st[x] > 0 or fa[x] == -1)return x;
    else return fa[x] = found(fa[x]);
}

map<pair<int,int>,bool>S;
void init(int x){
    for(auto s:h[x]){
        depth[s] = depth[x] + 1;
        init(s);
    }
    return ;
}
int cmp(pair<int,int>a, pair<int,int>b){
    return depth[a.first]>depth[b.first];
}
void solve(){
    memset(fa,-1,sizeof fa);
    read(n);read(k);read(m);
    rep(i,1,k){
        read(u);read(v);
        fa[v] = u;
        h[u].pb(v);
    }
    rep(i,1,n)if(fa[i] == -1)init(i);
    rep(i,1,m){
        read(u);read(v);
        st[u]++;
        G[v].pb(u);
        a[i] = {u,v};
    }
    sort(a+1,a+1+m,cmp);int cnt = 0;
    rep(i,1,m){
        int now = found(a[i].second);
        if(vis[a[i].second])continue;
        vis[a[i].second] = true;
        for(auto s:G[a[i].second])st[s]--;
        if(ok[now])continue;
        //printf("%d %d\n",a[i].first,a[i].second);
        //printf("%d\n",now);
        //printf("%d %d\n",a[i].first,a[i].second);
        cnt++;ok[now] = true;
    }
    write(cnt);pc('\n');
}


signed main(){solve();return 0; }

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。